 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Functii integrabile - Partea I
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 18 Feb 2008, nivel de dificultate  . .
Introducere: idea de a calcula aria unei figure plane ca limita de arii de reuniuni finite de dreptunghiuri; scurt istoric. Diviziuni si sume Riemann: definitie, exemple. Definitia integralei Riemann, exemple. Teorema: orice functie integrabila este marginita, demonstratie si exemplu. Formula Leibniz-Newton: demonstratie si exemple.
Domenii: Functii integrabile Riemann
FUNCŢII INTEGRABILE
Un punct de plecare pentru teoria care urmează este problema ariei figurilor geometrice. Vom spune că aria unei mulţimi care este reuniunea unei familii finite de dreptunghiuri care, două câte două, care au în comun cel mult segmente, este suma ariilor dreptunghiurilor componente.
Figuri simple precum triunghiul sau trapezul nu se încadrează în definiţia precedentă şi pentru aria unor asemenea figuri s-au propus formulele obţinute printr-o limită într-un proces de aproximare cu reuniuni de dreptunghiuri sau s-au propus formule care au calitatea că nu contrazic definiţia anterior acceptată pentru aria unui dreptunghi.
În acest capitol, consideraţii intuitive despre aria unei mulţimi de forma 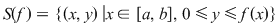 , unde , unde 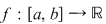 vor conduce la o clasă nouă de funcţii, aşa numitele funcţii integrabile. vor conduce la o clasă nouă de funcţii, aşa numitele funcţii integrabile.
Istoric vorbind, asemenea preocupări apar pentru prima dată la Arhimede care, pentru funcţia 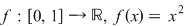 considera un sistem de puncte echidistante considera un sistem de puncte echidistante 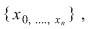
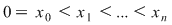 şi propunea aproximarea ariei subgraficului funcţiei şi propunea aproximarea ariei subgraficului funcţiei 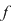 cu suma ariilor unor dreptunghiuri, ca în figură : cu suma ariilor unor dreptunghiuri, ca în figură : 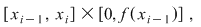 deci cu deci cu 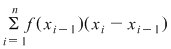
Materiale Didactice Asemanatoare
 Functii integrabile - Partea II Functii integrabile - Partea II
 Functii integrabile - Partea III Functii integrabile - Partea III
 Functii integrabile - Partea IV Functii integrabile - Partea IV
 Functii integrabile - Partea V Functii integrabile - Partea V
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|