| |
 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Functii integrabile - Partea IV
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 25 Feb 2008, nivel de dificultate  . .
Proprietati ale functiilor integrabile si ale integralei (continuare): orice functie monotona este integrabila; orice functie continua pe un interval inchis si marginit este uniform continua si integrabila; exemplu.
Domenii: Functii integrabile Riemann
Funcţii integrabile
(4)
Clase de funcţii integrabile
Caracterul calitativ al criteriului lui Darboux se reflectă în consecinţele următoare, în care se stabilesc unele familii de funcţii integrabile.
Teorema 1: Orice funcţie monotonă este integrabilă.
Demonstraţie:
Să presupunem că funcţia 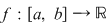 este crescătoare. Atunci, pentru orice este crescătoare. Atunci, pentru orice 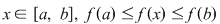 şi deci funcţia şi deci funcţia 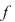 este mărginită. este mărginită.
Dacă 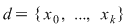 este o diviziunea intervalului este o diviziunea intervalului 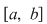 , atunci cu notaţiile uzuale avem , atunci cu notaţiile uzuale avem 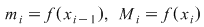 şi deci şi deci
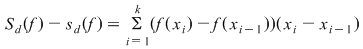 . .
Deoarece 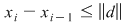 avem avem 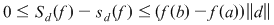 . .
În fine, dacă 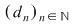 este un şir de diviziuni cu este un şir de diviziuni cu 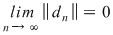 , din inegalităţile precedente rezultă că , din inegalităţile precedente rezultă că 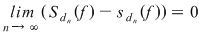 . Conform criteriului lui Darboux, funcţia . Conform criteriului lui Darboux, funcţia 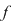 este integrabilă. este integrabilă.
Definiţie: Funcţia 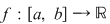 se numeşte uniform continuă dacă pentru orice se numeşte uniform continuă dacă pentru orice 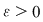 există există 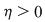 şi pentru orice şi pentru orice 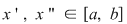 astfel încât astfel încât 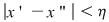 avem avem 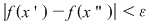 . .
Materiale Didactice Asemanatoare
 Functii integrabile - Partea I Functii integrabile - Partea I
 Functii integrabile - Partea II Functii integrabile - Partea II
 Functii integrabile - Partea III Functii integrabile - Partea III
 Functii integrabile - Partea V Functii integrabile - Partea V
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|
| |
| |