 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Functii integrabile - Partea V
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 25 Feb 2008, nivel de dificultate  . .
Proprietati ale functiilor integrabile si ale integralei (continuare): orice functie continua admite primitive, exemple, corolare: formula de medie, proprietatea de inertie a integralei, exemplu; modulul integralei e mai mic sau egal decat integrala modulului.
Domenii: Functii integrabile Riemann
Funcţii integrabile
(5)
Integrarea funcţiilor continue
În continuare se vor prezenta proprietăţi ale integralei funcţiilor continue, unele dintre aceste proprietăţi fiind adevărate şi pentru funcţii integrabile nu neapărat continue.
Reamintim că funcţiile studiate sunt definite pe un interval de forma 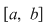 cu cu 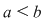 . .
Teorema 1: Orice funcţie continuă 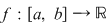 admite primitive. admite primitive.
Demonstraţie: Putem considera funcţia 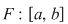 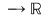 definită prin definită prin 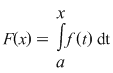 . Amintim că prin convenţie . Amintim că prin convenţie 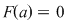 . .
Vom arăta că funcţia 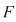 este o primitivă a funcţiei este o primitivă a funcţiei 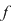 . Fie pentru aceasta . Fie pentru aceasta 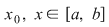 , , 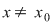 . Să presupunem spre exemplu că . Să presupunem spre exemplu că 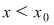 . Atunci: . Atunci:
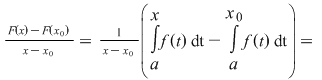
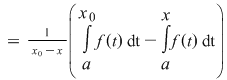 . Rezultă atunci . Rezultă atunci 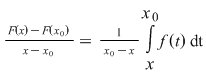 , de unde , de unde 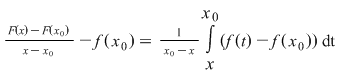 (1) (1)
Funcţia 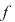 fiind continuă în punctul fiind continuă în punctul 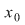 , pentru orice , pentru orice 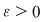 , există , există 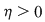 astfel încât dacă astfel încât dacă 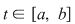 şi şi 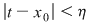 avem avem 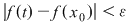 . Atunci, dacă . Atunci, dacă 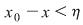 şi şi 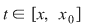 , avem , avem 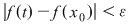 . Rezultă că . Rezultă că 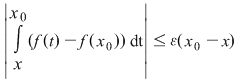 şi atunci din (1) rezultă: şi atunci din (1) rezultă: 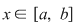 , , 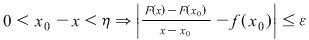 . .
Materiale Didactice Asemanatoare
 Functii integrabile - Partea I Functii integrabile - Partea I
 Functii integrabile - Partea II Functii integrabile - Partea II
 Functii integrabile - Partea III Functii integrabile - Partea III
 Functii integrabile - Partea IV Functii integrabile - Partea IV
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|