 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Functii integrabile - Partea II
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 18 Feb 2008, nivel de dificultate  . .
Criterii de integrabilitate: criteriul cu siruri de sume Riemann, demonstratie; proprietati ale functiilor integrabile si ale integralei, exemple; sume Darboux, definitie si proprietati; criteriul lui Darboux: demonstratie si exemple; aplicatii.
Domenii: Functii integrabile Riemann
Funcţii integrabile
(2)
Criterii de integrabilitate.
Cu ajutorul condiţiilor echivalente de integrabilitate se vor putea obţine proprietăţi ale funcţiilor integrabile şi ale integralei, se vor identifica familii de funcţii integrabile.
2.1. Criteriul cu şiruri de sume Riemann.
Teoremă: (criteriul cu siruri de sume Riemann)
Funcţia 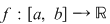 este integrabilă dacă şi numai dacă există un număr real este integrabilă dacă şi numai dacă există un număr real 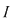 şi pentru orice şir şi pentru orice şir 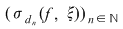 de sume Riemann astfel încât de sume Riemann astfel încât 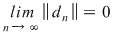 avem avem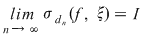 . Atunci . Atunci 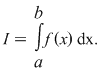
Demonstratie:
Dacă funcţia 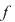 este integrabilă, atunci există un număr real este integrabilă, atunci există un număr real 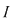 şi pentru orice număr şi pentru orice număr 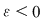 există există 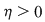 astfel încât pentru orice sumă Riemann astfel încât pentru orice sumă Riemann 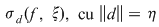 , avem , avem 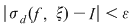 . Atunci, dacă . Atunci, dacă 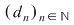 este un şir de diviziuni cu este un şir de diviziuni cu 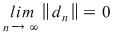 , există , există 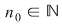 şi pentru orice şi pentru orice 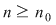 , avem , avem 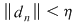 . Rezultă că . Rezultă că 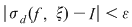 . Recapitulând, pentru orice . Recapitulând, pentru orice 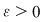 există există 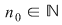 astfel încât pentru orice astfel încât pentru orice 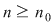 avem avem 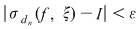 . Aceasta înseamnă . Aceasta înseamnă 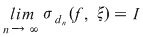 . .
Reciproc, să presupunem că există un număr real 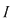 şi că pentru orice şir de sume Riemann şi că pentru orice şir de sume Riemann 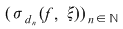 , cu , cu 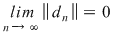 avem avem 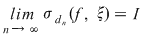 . Să presupunem că funcţia . Să presupunem că funcţia 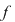 nu este integrabilă. Atunci, pentru numărul nu este integrabilă. Atunci, pentru numărul 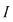 există există 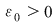 şi, pentru orice număr şi, pentru orice număr 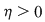 , există o sumă Riemann , există o sumă Riemann 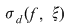 cu cu 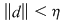 , astfel încât , astfel încât 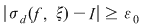 . Alegând . Alegând 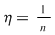 , rezultă că există , rezultă că există 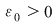 şi pentru orice şi pentru orice 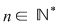 , există , există 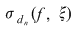 o sumă Riemann cu o sumă Riemann cu 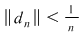 , astfel încât , astfel încât 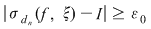 . Atunci şirul . Atunci şirul 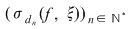 nu converge către nu converge către 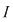 , cu toate că , cu toate că 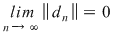 , ceea ce contrazice ipoteza. Funcţia , ceea ce contrazice ipoteza. Funcţia 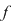 este integrabilă şi este integrabilă şi 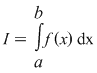 . .
Materiale Didactice Asemanatoare
 Functii integrabile - Partea I Functii integrabile - Partea I
 Functii integrabile - Partea III Functii integrabile - Partea III
 Functii integrabile - Partea IV Functii integrabile - Partea IV
 Functii integrabile - Partea V Functii integrabile - Partea V
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|