 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Functii integrabile - Partea IV
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 25 Feb 2008, nivel de dificultate  . .
Proprietati ale functiilor integrabile si ale integralei (continuare): orice functie monotona este integrabila; orice functie continua pe un interval inchis si marginit este uniform continua si integrabila; exemplu.
Domenii: Functii integrabile Riemann
Se observă că orice funcţie uniform continuă este continuă în orice punct. De fapt, în cazul particular considerat în definiţie este adevărată şi afirmaţia reciprocă:
Propoziţia 1: Orice funcţie continuă pe un interval închis şi mărginit este uniform continuă.
Demonstraţie:
Fie 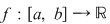 o funcţie continuă. Să presupunem prin absurd că funcţia nu e uniform continuă. Există atunci o funcţie continuă. Să presupunem prin absurd că funcţia nu e uniform continuă. Există atunci 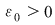 şi pentru orice şi pentru orice 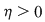 , există , există 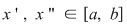 , astfel încât , astfel încât 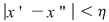 şi şi 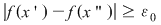 . .
În particular, pentru 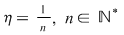 , există , există 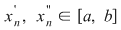 astfel încât astfel încât 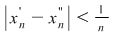 şi şi 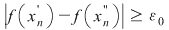 . Şirul . Şirul 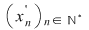 fiind mărginit, există un subşir convergent fiind mărginit, există un subşir convergent 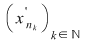 . Din . Din 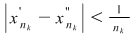 rezultă că rezultă că 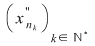 este de asemenea convergent şi este de asemenea convergent şi 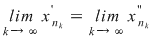 . Fie . Fie 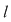 această limită comună. Atunci această limită comună. Atunci 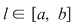 , iar relaţia , iar relaţia 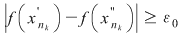 contrazice continuitatea funcţiei contrazice continuitatea funcţiei 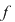 în punctul în punctul 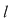 . .
Teorema 2: Orice funcţie continuă 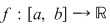 este integrabilă. este integrabilă.
Demonstraţie:
Vom arăta că funcţia 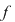 este integrabilă folosind criteriul lui Darboux. Fie este integrabilă folosind criteriul lui Darboux. Fie 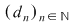 un şir de diviziuni cu un şir de diviziuni cu 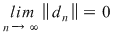 . Pentru a arăta că . Pentru a arăta că 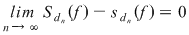 , fie , fie 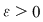
Deoarece conform propoziţiei precedente funcţia 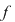 este uniform continuă, există este uniform continuă, există 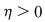 astfel încât dacă astfel încât dacă 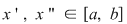 şi şi 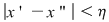 , atunci , atunci 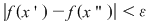 . Deoarece . Deoarece 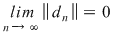 , există , există 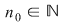 şi pentru orice şi pentru orice 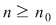 avem avem 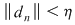 . Dacă punctele diviziunii . Dacă punctele diviziunii 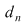 sunt notate sunt notate 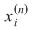 , atunci pentru , atunci pentru 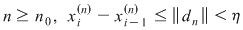 . Atunci pentru orice puncte . Atunci pentru orice puncte 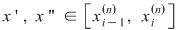 avem avem 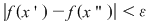 . Dacă . Dacă 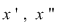 sunt puncte din sunt puncte din 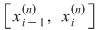 în care funcţia în care funcţia 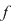 îşi atinge marginile: îşi atinge marginile:
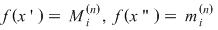 , atunci , atunci 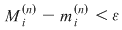 şi deci, pentru şi deci, pentru 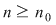 avem avem 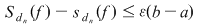 . Aceasta arată că . Aceasta arată că 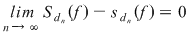 şi deci funcţia este integrabilă. şi deci funcţia este integrabilă.
Materiale Didactice Asemanatoare
 Functii integrabile - Partea I Functii integrabile - Partea I
 Functii integrabile - Partea II Functii integrabile - Partea II
 Functii integrabile - Partea III Functii integrabile - Partea III
 Functii integrabile - Partea V Functii integrabile - Partea V
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|