 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Functii integrabile - Partea II
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 18 Feb 2008, nivel de dificultate  . .
Criterii de integrabilitate: criteriul cu siruri de sume Riemann, demonstratie; proprietati ale functiilor integrabile si ale integralei, exemple; sume Darboux, definitie si proprietati; criteriul lui Darboux: demonstratie si exemple; aplicatii.
Domenii: Functii integrabile Riemann
2.2 Criteriul lui Darboux.
Sume Darboux
Reamintim că marginea inferioară a unei mulţimi minorate este cel mai mare minorant al acestei mulţimi şi că marginea superioară a unei mulţimi majorate este cel mai mic majorant. Pentru mulţimea mărginită 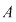 acestea se notează acestea se notează 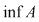 , respectiv , respectiv 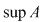 . .
Fie 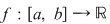 o funcţie mărginită. Fie o funcţie mărginită. Fie 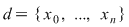 o diviziune a intervalului o diviziune a intervalului 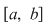 şi pentru fiecare interval şi pentru fiecare interval 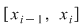 , fie , fie 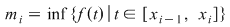 , , 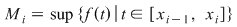 . Aceste numere sunt, deci, marginea inferioară, respectiv superioară a mulţimii . Aceste numere sunt, deci, marginea inferioară, respectiv superioară a mulţimii 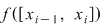 . Se notează: . Se notează: 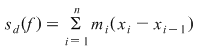 şi şi 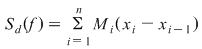 şi se numesc suma Darboux inferioară, respectiv superioară, asociate funcţiei şi se numesc suma Darboux inferioară, respectiv superioară, asociate funcţiei 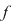 şi diviziunii şi diviziunii 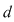 . .
Un produs de forma 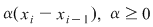 , poate fi considerat ca aria unui dreptunghi cu laturile de lungimi , poate fi considerat ca aria unui dreptunghi cu laturile de lungimi 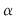 şi şi 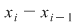 . Atunci, pentru cazul unei funcţii pozitive, sumele Darboux constituie nişte sume de arii de dreptunghiuri ilustrate ca mai jos: . Atunci, pentru cazul unei funcţii pozitive, sumele Darboux constituie nişte sume de arii de dreptunghiuri ilustrate ca mai jos:
Materiale Didactice Asemanatoare
 Functii integrabile - Partea I Functii integrabile - Partea I
 Functii integrabile - Partea III Functii integrabile - Partea III
 Functii integrabile - Partea IV Functii integrabile - Partea IV
 Functii integrabile - Partea V Functii integrabile - Partea V
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|