 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Functii integrabile - Partea II
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 18 Feb 2008, nivel de dificultate  . .
Criterii de integrabilitate: criteriul cu siruri de sume Riemann, demonstratie; proprietati ale functiilor integrabile si ale integralei, exemple; sume Darboux, definitie si proprietati; criteriul lui Darboux: demonstratie si exemple; aplicatii.
Domenii: Functii integrabile Riemann
Exemple:
1) Dacă 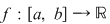 este o funcţie crescătoare, atunci este o funcţie crescătoare, atunci 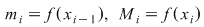 , , 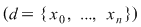 şi şi 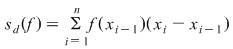 , , 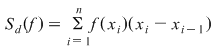 . .
2) Fie 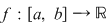 o funcţie continuă şi o funcţie continuă şi 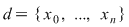 o diviziune a intervalului o diviziune a intervalului 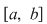 . Se ştie că funcţia . Se ştie că funcţia 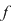 este atunci mărginită şi îşi atinge marginile pe orice interval inclus în este atunci mărginită şi îşi atinge marginile pe orice interval inclus în 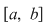 şi, deci, în particular, există numerele şi, deci, în particular, există numerele 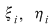 în în 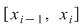 astfel încât astfel încât 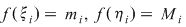 . .
Atunci: 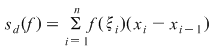 , , 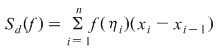 . .
Se observă deci că, în acest caz, sumele Darboux sunt cazuri particulare de sume Riemann.
3) Fie 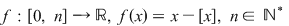 . Fie . Fie 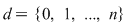 . Dacă . Dacă 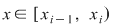 atunci atunci 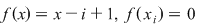 . Atunci . Atunci 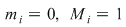 şi deci şi deci 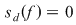 şi şi 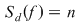 . Suma . Suma 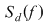 nu este sumă Riemann. nu este sumă Riemann.
Propoziţia 3: Dacă 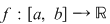 este o funcţie măginită, iar este o funcţie măginită, iar 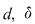 sunt diviziuni ale intervalului sunt diviziuni ale intervalului 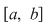 astfel încât astfel încât 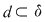 , atunci , atunci 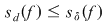 şi şi 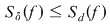 . .
Demonstraţie:
Să arătăm, spre exemplu, că 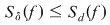 . Dacă . Dacă 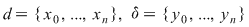 vom analiza contribuţia unui interval vom analiza contribuţia unui interval 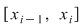 la sumele Darboux la sumele Darboux 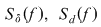 . Conform ipotezei . Conform ipotezei 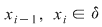 şi în şi în 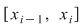 se pot afla şi alte puncte din se pot afla şi alte puncte din 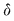 . Dacă în . Dacă în 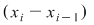 nu se mai află alte puncte din nu se mai află alte puncte din 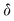 , atunci contribuţia intervalului , atunci contribuţia intervalului 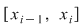 la sumele Darboux considerate este aceeaşi: la sumele Darboux considerate este aceeaşi: 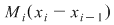 . Dacă în . Dacă în 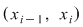 se află şi alte puncte din se află şi alte puncte din 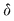 , să considerăm cazul cel mai simplu, în care în , să considerăm cazul cel mai simplu, în care în 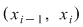 se mai află doar punctul se mai află doar punctul  . Contribuţia intervalului . Contribuţia intervalului 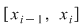 la la 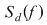 este este 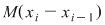 , iar contribuţia la , iar contribuţia la 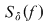 este este 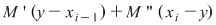 , unde , unde 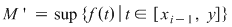 , , 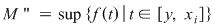 . Deoarece . Deoarece 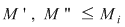 , rezultă că , rezultă că 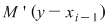 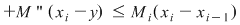 . O asemenea inegalitate este adevărată şi dacă în . O asemenea inegalitate este adevărată şi dacă în 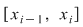 se află mai multe puncte din se află mai multe puncte din 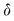 . Rezultă că . Rezultă că 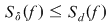 . .
Materiale Didactice Asemanatoare
 Functii integrabile - Partea I Functii integrabile - Partea I
 Functii integrabile - Partea III Functii integrabile - Partea III
 Functii integrabile - Partea IV Functii integrabile - Partea IV
 Functii integrabile - Partea V Functii integrabile - Partea V
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|