| |
 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Functii integrabile - Partea V
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 25 Feb 2008, nivel de dificultate  . .
Proprietati ale functiilor integrabile si ale integralei (continuare): orice functie continua admite primitive, exemple, corolare: formula de medie, proprietatea de inertie a integralei, exemplu; modulul integralei e mai mic sau egal decat integrala modulului.
Domenii: Functii integrabile Riemann
Exemple:
1) Fie 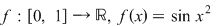 şi şi 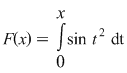 . Atunci . Atunci 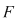 este derivabilă şi este derivabilă şi 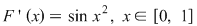 . .
2) Să studiem derivabilitatea funcţiei 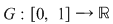 , , 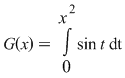 . Deoarece . Deoarece 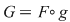 unde unde 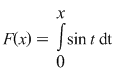 , iar , iar 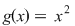 , rezultă că , rezultă că 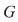 este derivabilă şi este derivabilă şi 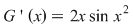 . .
Corolarul 1: Fie 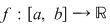 o funcţie continuă. Există atunci o funcţie continuă. Există atunci 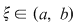 astfel încât: astfel încât: 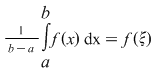 . .
Demonstraţie:
Funcţia 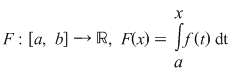 este derivabilă şi are loc este derivabilă şi are loc 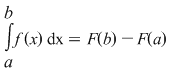 . Conform teoremei lui Lagrange, există . Conform teoremei lui Lagrange, există 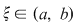 astfel încât astfel încât 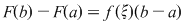 . .
Materiale Didactice Asemanatoare
 Functii integrabile - Partea I Functii integrabile - Partea I
 Functii integrabile - Partea II Functii integrabile - Partea II
 Functii integrabile - Partea III Functii integrabile - Partea III
 Functii integrabile - Partea IV Functii integrabile - Partea IV
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|
| |
| |