| |
 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Functii integrabile - Partea V
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 25 Feb 2008, nivel de dificultate  . .
Proprietati ale functiilor integrabile si ale integralei (continuare): orice functie continua admite primitive, exemple, corolare: formula de medie, proprietatea de inertie a integralei, exemplu; modulul integralei e mai mic sau egal decat integrala modulului.
Domenii: Functii integrabile Riemann
Exemplu:
Conform corolarului1, există
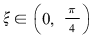 , , 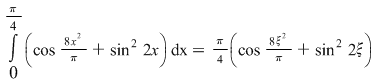 . .
Rezultă că 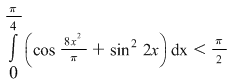 . .
Propoziţia 1: Fie 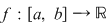 o funcţie continuă. Atunci o funcţie continuă. Atunci 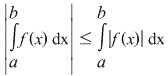 . .
Demonstraţie:
Se ştie că dacă funcţia 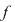 este continuă, atunci funcţia este continuă, atunci funcţia 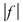 definită prin definită prin 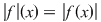 este, de asemenea, continuă şi este, deci, integrabilă. Pentru orice este, de asemenea, continuă şi este, deci, integrabilă. Pentru orice 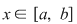 are loc: are loc:
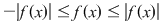 . .
Din monotonia integralei, rezultă atunci:
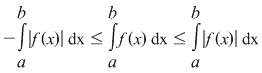 . .
Materiale Didactice Asemanatoare
 Functii integrabile - Partea I Functii integrabile - Partea I
 Functii integrabile - Partea II Functii integrabile - Partea II
 Functii integrabile - Partea III Functii integrabile - Partea III
 Functii integrabile - Partea IV Functii integrabile - Partea IV
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|
| |
| |