 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Functii integrabile - Partea I
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 18 Feb 2008, nivel de dificultate  . .
Introducere: idea de a calcula aria unei figure plane ca limita de arii de reuniuni finite de dreptunghiuri; scurt istoric. Diviziuni si sume Riemann: definitie, exemple. Definitia integralei Riemann, exemple. Teorema: orice functie integrabila este marginita, demonstratie si exemplu. Formula Leibniz-Newton: demonstratie si exemple.
Domenii: Functii integrabile Riemann
Procedeul de definiţie era un proces limită în care, folosind o formulă de calcul pentru suma unei progresii geometrice infinite, Arhimede ajungea la concluzia că aria este 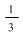 . .
Era deci o abordare a problemei într-un caz particular. Procedeul este reluat de Cauchy în 1823 care, cu acelaşi tip de sume, l-a extins la clasa funcţiilor continue. Riemann consideră sume mai generale şi defineşte o nouă clasă de funcţii, acelea pentru care un proces asemănător celui precedent este convergent.
 1.FUNCŢII INTEGRABILE
1.FUNCŢII INTEGRABILE
1.1Diviziuni, sume Riemann
Fie 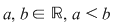
Definiţia 1: Se numeşte diviziune a intervalului 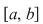 orice mulţime finită orice mulţime finită 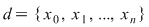 astfel încât astfel încât 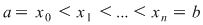
Se notează cu 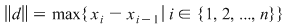 şi se numeşte norma diviziunii şi se numeşte norma diviziunii 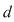 . .
Observaţie: Intervalele 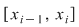 se numesc intervale ale diviziunii se numesc intervale ale diviziunii 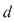 şi, prin urmare, norma unei diviziuni este cea mai mare lungime a intervalelor din diviziune. şi, prin urmare, norma unei diviziuni este cea mai mare lungime a intervalelor din diviziune.
Exemple :
1) Fie 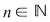 , , 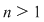 şi şi 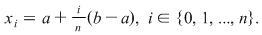 Mulţimea Mulţimea 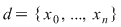 este o diviziune a intervalului este o diviziune a intervalului 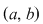 formată din puncte echidistante. Norma acestei diviziuni este formată din puncte echidistante. Norma acestei diviziuni este 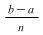 . .
2) Mulţimea 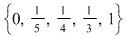 este o diviziune a intervalului este o diviziune a intervalului 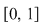 . Norma acestei diviziuni este . Norma acestei diviziuni este 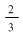 . .
3) Mulţimea 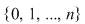 este o diviziune a intervalului este o diviziune a intervalului 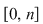 , norma ei fiind , norma ei fiind 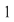 . .
4) Mulţimea 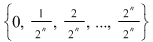 este o diviziune de normă este o diviziune de normă 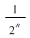 a intervalului a intervalului 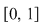 . .
Definiţie 2: Fie 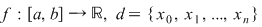 o diviziune a intervalului o diviziune a intervalului 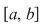 şi şi 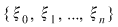 un sistem de puncte astfel încât un sistem de puncte astfel încât 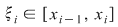 . Numărul . Numărul 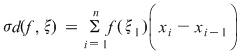 se numeşte sumă Riemann asociată funcţiei se numeşte sumă Riemann asociată funcţiei 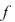 , diviziunii , diviziunii 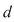 şi sistemului de puncte intermediare şi sistemului de puncte intermediare 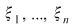 . .
Materiale Didactice Asemanatoare
 Functii integrabile - Partea II Functii integrabile - Partea II
 Functii integrabile - Partea III Functii integrabile - Partea III
 Functii integrabile - Partea IV Functii integrabile - Partea IV
 Functii integrabile - Partea V Functii integrabile - Partea V
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|