 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Functii integrabile - Partea II
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 18 Feb 2008, nivel de dificultate  . .
Criterii de integrabilitate: criteriul cu siruri de sume Riemann, demonstratie; proprietati ale functiilor integrabile si ale integralei, exemple; sume Darboux, definitie si proprietati; criteriul lui Darboux: demonstratie si exemple; aplicatii.
Domenii: Functii integrabile Riemann
Atunci, pentru orice 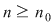 , avem , avem 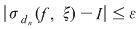 sau sau 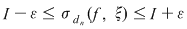 . Din observaţia 3 rezultă că, pentru orice . Din observaţia 3 rezultă că, pentru orice 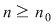 , , 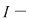 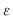  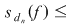 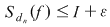 .Atunci, pentru orice .Atunci, pentru orice 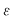 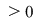 , există , există 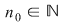 astfel încât pentru orice astfel încât pentru orice 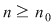 avem avem 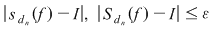 , adică , adică 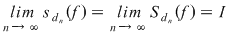 . .
Teoremă (Criteriul lui Darboux): Funcţia 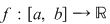 este integrabilă Riemann dacă şi numai dacă este mărginită şi pentru orice şir de diviziuni este integrabilă Riemann dacă şi numai dacă este mărginită şi pentru orice şir de diviziuni 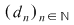 cu cu 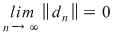 avem avem 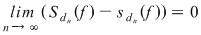 . .
Demonstraţie:
Dacă funcţia 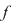 este integrabilă, din propoziţia precedentă rezultă că pentru orice şir de diviziuni este integrabilă, din propoziţia precedentă rezultă că pentru orice şir de diviziuni 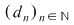 cu cu 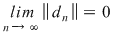 avem avem 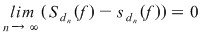 . Reciproc, să presupunem că pentru orice şir . Reciproc, să presupunem că pentru orice şir 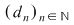 de diviziuni cu de diviziuni cu 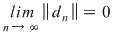 avem avem 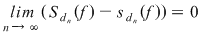 . Vom arăta, pentru început, că există . Vom arăta, pentru început, că există 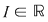 astfel încât de îndată ce astfel încât de îndată ce 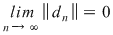 să rezulte să rezulte 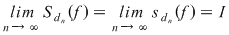 . Fie, mai întâi, un şir . Fie, mai întâi, un şir 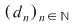 cu proprietăţile: cu proprietăţile: 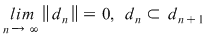 pentru orice pentru orice 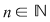 . Şirul . Şirul 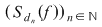 este atunci descrescător, iar şirul este atunci descrescător, iar şirul 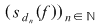 este crescător. Ambele şiruri fiind mărginite, ele sunt deci convergente, iar din ipoteză rezultă că este crescător. Ambele şiruri fiind mărginite, ele sunt deci convergente, iar din ipoteză rezultă că 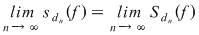 . Notăm cu . Notăm cu 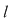 această limită comună. Avem şi această limită comună. Avem şi 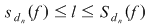 . Dacă . Dacă 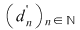 este un alt şir de diviziuni, cu proprietăţile puse mai sus: este un alt şir de diviziuni, cu proprietăţile puse mai sus: 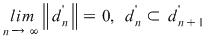 pentru orice pentru orice 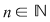 , notăm corespunzător , notăm corespunzător 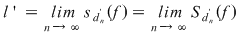 . .
Materiale Didactice Asemanatoare
 Functii integrabile - Partea I Functii integrabile - Partea I
 Functii integrabile - Partea III Functii integrabile - Partea III
 Functii integrabile - Partea IV Functii integrabile - Partea IV
 Functii integrabile - Partea V Functii integrabile - Partea V
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|