 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Functii integrabile - Partea II
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 18 Feb 2008, nivel de dificultate  . .
Criterii de integrabilitate: criteriul cu siruri de sume Riemann, demonstratie; proprietati ale functiilor integrabile si ale integralei, exemple; sume Darboux, definitie si proprietati; criteriul lui Darboux: demonstratie si exemple; aplicatii.
Domenii: Functii integrabile Riemann
Atunci şirul 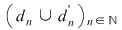 are şi el cele două proprietăţi menţionate. Din are şi el cele două proprietăţi menţionate. Din 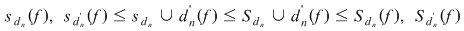 rezultă că rezultă că 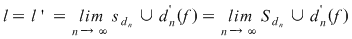 . În concluzie, există . În concluzie, există  astfel încât pentru orice şir de diviziuni astfel încât pentru orice şir de diviziuni 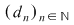 cu proprietăţile cu proprietăţile 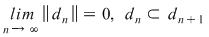 pentru orice pentru orice 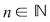 , avem , avem 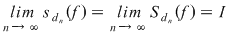 . .
Este important să reţinem că 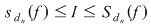 . Fie acum . Fie acum 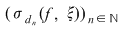 un şir de sume Riemann corespunzător unui şir un şir de sume Riemann corespunzător unui şir 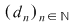 de diviziuni cu de diviziuni cu 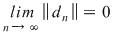 . Fie . Fie 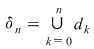 . Şirul de diviziuni . Şirul de diviziuni 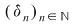 are proprietăţile: are proprietăţile: 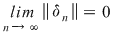 , aceasta deoarece , aceasta deoarece 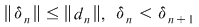 . Atunci . Atunci 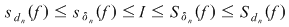 , de unde rezultă că , de unde rezultă că 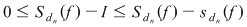 . Din ipoteză rezultă că . Din ipoteză rezultă că 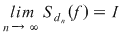 . .
Analog, 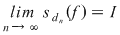 . În fine, deoarece . În fine, deoarece 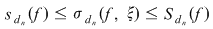 , va rezulta că , va rezulta că 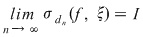 , deci funcţia , deci funcţia 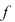 este integrabilă. este integrabilă.
Observaţii:
1) Teorema precedentă dă o condiţie necesară şi suficientă de integrabilitate exprimată doar prin valorile funcţiei.
2) Afirmaţia următoare este o variantă a teoremei precedente:
Teoremă: Funcţia 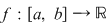 este integrabilă dacă şi numai dacă este mărginită şi pentru orice este integrabilă dacă şi numai dacă este mărginită şi pentru orice 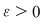 există există 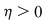 astfel încât pentru orice diviziune astfel încât pentru orice diviziune 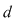 cu cu 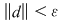 , avem , avem 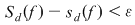 . .
3) Se poate demonstra şi următorul criteriu:
Teoremă: Funcţia 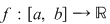 este integrabilă dacă şi numai dacă pentru orice este integrabilă dacă şi numai dacă pentru orice 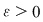 există o diviziune există o diviziune 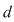 astfel încât astfel încât 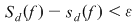 . .
Materiale Didactice Asemanatoare
 Functii integrabile - Partea I Functii integrabile - Partea I
 Functii integrabile - Partea III Functii integrabile - Partea III
 Functii integrabile - Partea IV Functii integrabile - Partea IV
 Functii integrabile - Partea V Functii integrabile - Partea V
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|