 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Functii integrabile - Partea II
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 18 Feb 2008, nivel de dificultate  . .
Criterii de integrabilitate: criteriul cu siruri de sume Riemann, demonstratie; proprietati ale functiilor integrabile si ale integralei, exemple; sume Darboux, definitie si proprietati; criteriul lui Darboux: demonstratie si exemple; aplicatii.
Domenii: Functii integrabile Riemann
Observaţii:
1. Propoziţia precedentă spune că mulţimea funcţiilor integrabile este spaţiu vectorial real, iar aplicaţia care asociază fiecărei funcţii integrabile integrala sa este o aplicaţie liniară. În particular, dacă 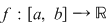 este integrabilă, iar este integrabilă, iar 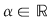 , atunci , atunci 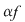 este integrabilă şi este integrabilă şi 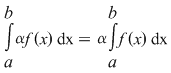 . .
2. Prin inducţie rezultă că dacă 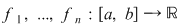 sunt funcţii integrabile, atunci sunt funcţii integrabile, atunci 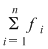 este integrabilă şi este integrabilă şi 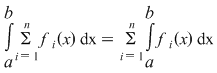 . .
Propoziţia 2: Dacă 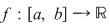 este o funcţie integrabilă şi este o funcţie integrabilă şi 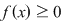 pentru orice pentru orice 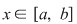 , atunci , atunci 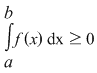 . .
Demonstraţie:
Din ipoteză rezultă că orice sumă Riemann asociată funcţiei 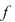 este un număr pozitiv. Dacă este un număr pozitiv. Dacă 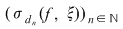 este un şir de sume Riemann cu proprietatea este un şir de sume Riemann cu proprietatea 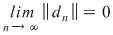 , atunci limita sa, adică , atunci limita sa, adică 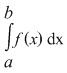 este, de asemenea, un număr pozitiv. este, de asemenea, un număr pozitiv.
Materiale Didactice Asemanatoare
 Functii integrabile - Partea I Functii integrabile - Partea I
 Functii integrabile - Partea III Functii integrabile - Partea III
 Functii integrabile - Partea IV Functii integrabile - Partea IV
 Functii integrabile - Partea V Functii integrabile - Partea V
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|