 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Functii integrabile - Partea III
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 18 Feb 2008, nivel de dificultate  . .
Proprietati ale functiilor integrabile si ale integralei (continuare): aditivitatea integralei, exemple; restrictia unei functii integrabila este integrabila; exemple.
Domenii: Functii integrabile Riemann
Propoziţia 2: Dacă pentru funcţia 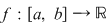 există există 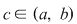 astfel încât restricţiile funcţiei astfel încât restricţiile funcţiei 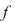 la intervalele la intervalele 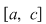 şi şi 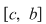 sunt integrabile, atunci funcţia sunt integrabile, atunci funcţia 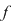 este integrabilă. este integrabilă.
Demonstraţie:
Din ipoteză rezultă că funcţia  este mărginită. Fie este mărginită. Fie 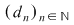 un şir de diviziuni pentru intervalul un şir de diviziuni pentru intervalul 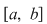 astfel încât astfel încât 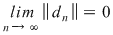 . Vom arăta că . Vom arăta că 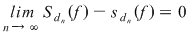 şi vom aplica criteriul lui Darboux. Fie şi vom aplica criteriul lui Darboux. Fie 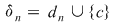 şi şi 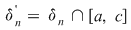 , , 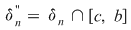 . Prin adăugarea punctului . Prin adăugarea punctului  am obţinut pentru intervalele am obţinut pentru intervalele 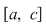 respectiv respectiv 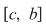 diviziunile diviziunile 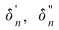 . Avem, evident, . Avem, evident, 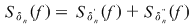 . (1) . (1)
Conform ipotezei avem 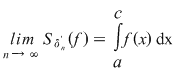 , ,  . Din (1) rezultă că . Din (1) rezultă că  . Analog se arată că şirul . Analog se arată că şirul 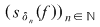 are aceeaşi limită şi deci are aceeaşi limită şi deci 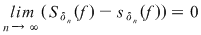 . Dacă . Dacă  , atunci , atunci  şi deci diferenţa şi deci diferenţa  este zero. În caz contrar, dacă este zero. În caz contrar, dacă 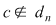 , notând , notând 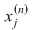 punctele diviziunii punctele diviziunii 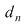 , există un interval , există un interval 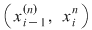 astfel încât astfel încât  . Atunci . Atunci

 , unde , unde  , , 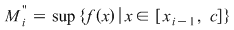 , , 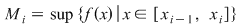 . .
Materiale Didactice Asemanatoare
 Functii integrabile - Partea I Functii integrabile - Partea I
 Functii integrabile - Partea II Functii integrabile - Partea II
 Functii integrabile - Partea IV Functii integrabile - Partea IV
 Functii integrabile - Partea V Functii integrabile - Partea V
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|