| |
 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Functii integrabile - Partea I
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 18 Feb 2008, nivel de dificultate  . .
Introducere: idea de a calcula aria unei figure plane ca limita de arii de reuniuni finite de dreptunghiuri; scurt istoric. Diviziuni si sume Riemann: definitie, exemple. Definitia integralei Riemann, exemple. Teorema: orice functie integrabila este marginita, demonstratie si exemplu. Formula Leibniz-Newton: demonstratie si exemple.
Domenii: Functii integrabile Riemann
Teorema 1: (formula Leibniz-Newton)
Fie 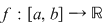 o funţie integrabilă, care admite primitive şi fie o funţie integrabilă, care admite primitive şi fie 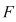 o primitivă a sa. Atunci : o primitivă a sa. Atunci : 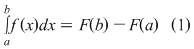
Demostraţie: Conform ipotezei , pentru orice 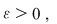 există există 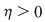 astfel încât pentru orice sumă Riemann astfel încât pentru orice sumă Riemann 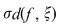 cu cu 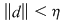 avem : avem : 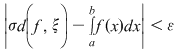
Fie 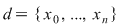 o diviziune a intervalului o diviziune a intervalului 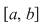 cu cu 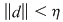 . Conform teoremei lui Lagrange aplicată funcţiei . Conform teoremei lui Lagrange aplicată funcţiei 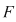 pe intervalul pe intervalul 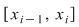 există există 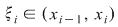 astfel încât astfel încât 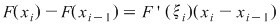 şi deci şi deci 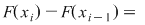 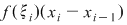 . .
Rezultă că 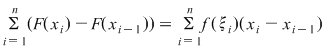 şi deci şi deci 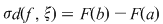 . Avem atunci . Avem atunci 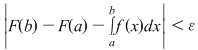 pentru orice pentru orice 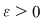 şi prin urmare şi prin urmare
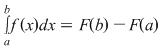 . .
Observaţii:
1. Formula (1) se scrie 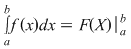 , iar membrul drept al egalităţii se citeşte , iar membrul drept al egalităţii se citeşte 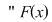 de la de la 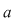 la la 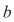 ". ".
2. Se poate arăta că: " dacă 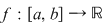 este o funcţie care admite primitive şi dacă este derivabilă cu derivata continuă, atunci funcţia este o funcţie care admite primitive şi dacă este derivabilă cu derivata continuă, atunci funcţia 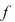 este integrabilă şi este integrabilă şi 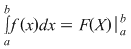 , unde , unde  este o primitivă a funcţiei este o primitivă a funcţiei  ". ".
Materiale Didactice Asemanatoare
 Functii integrabile - Partea II Functii integrabile - Partea II
 Functii integrabile - Partea III Functii integrabile - Partea III
 Functii integrabile - Partea IV Functii integrabile - Partea IV
 Functii integrabile - Partea V Functii integrabile - Partea V
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|
| |
| |