| |
 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Functii integrabile - Partea I
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 18 Feb 2008, nivel de dificultate  . .
Introducere: idea de a calcula aria unei figure plane ca limita de arii de reuniuni finite de dreptunghiuri; scurt istoric. Diviziuni si sume Riemann: definitie, exemple. Definitia integralei Riemann, exemple. Teorema: orice functie integrabila este marginita, demonstratie si exemplu. Formula Leibniz-Newton: demonstratie si exemple.
Domenii: Functii integrabile Riemann
Definiţie: Fie 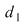 , ,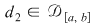 . Vom spune că diviziunea . Vom spune că diviziunea 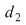 este mai fină decât este mai fină decât 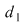
dacă 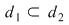 . Se spune şi că . Se spune şi că 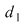 este mai puţin fină decât este mai puţin fină decât 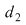 . .
Exemple:
1) Dacă 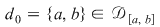 atunci atunci 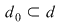 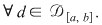
2) Pe intervalul 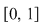 diviziunea diviziunea 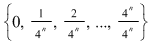 este mai fină decât este mai fină decât 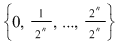 . .
Observaţii:
1. Diviziunea 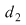 este mai fină decât este mai fină decât 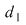 dacă şi numai dacă pentru orice interval dacă şi numai dacă pentru orice interval 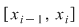 al lui al lui 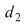 există există 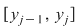 un interval din un interval din 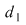 astfel încât astfel încât 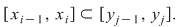
2. Dacă 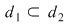 atunci atunci 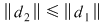 . Reciproca acestei afirmaţii nu este adevărată. Spre exemplu, dacă . Reciproca acestei afirmaţii nu este adevărată. Spre exemplu, dacă 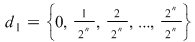 , , 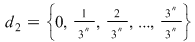 ,atunci ,atunci
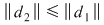 dar dar 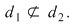
3. Dacă 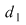 , ,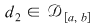 şi şi 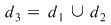 , atunci , atunci 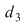 este mai fină decât este mai fină decât 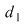 şi decât şi decât 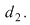
Definiţie: Un şir 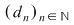 de diviziuni ale intervalului de diviziuni ale intervalului 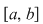 se numeşte crescător dacă se numeşte crescător dacă 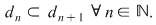
Exemplu:
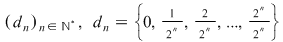
1.2 Funcţii integrabile
Fie 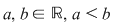 . .
Materiale Didactice Asemanatoare
 Functii integrabile - Partea II Functii integrabile - Partea II
 Functii integrabile - Partea III Functii integrabile - Partea III
 Functii integrabile - Partea IV Functii integrabile - Partea IV
 Functii integrabile - Partea V Functii integrabile - Partea V
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|
| |
| |