 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Functii integrabile - Partea I
Autor: Dana Schiopu
Descriere: articol pentru Clasa a XII-a publicat in data de 18 Feb 2008, nivel de dificultate  . .
Introducere: idea de a calcula aria unei figure plane ca limita de arii de reuniuni finite de dreptunghiuri; scurt istoric. Diviziuni si sume Riemann: definitie, exemple. Definitia integralei Riemann, exemple. Teorema: orice functie integrabila este marginita, demonstratie si exemplu. Formula Leibniz-Newton: demonstratie si exemple.
Domenii: Functii integrabile Riemann
Avem 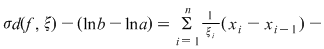
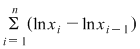 . Conform teoremei lui Lagrange aplicată funcţiei . Conform teoremei lui Lagrange aplicată funcţiei 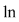 pe intervalul pe intervalul 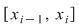 , există , există 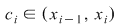 astfel încât astfel încât 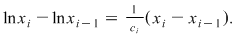
Rezultă că 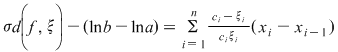 şi deci şi deci 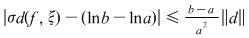 . Atunci, dacă . Atunci, dacă 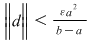 , avem , avem 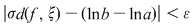 . .
Funcţia 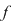 este deci integrabilă şi integrala ei este este deci integrabilă şi integrala ei este 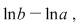 adică adică 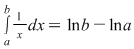
4) Amintim că funcţia 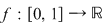 , , 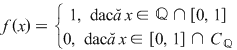
numită funcţia lui Dirichlet, este cunoscută ca fiind un exemplu de funcţie discontinuă în fiecare punct. Vom arăta că această funţie nu este integrabilă .
Să presupunem prin absurd că ar exista un număr real 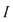 şi că pentru orice şi că pentru orice 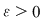 există există 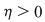 astfel încât pentru orice sumă Riemann astfel încât pentru orice sumă Riemann 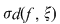 cu cu 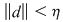 am avea am avea 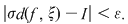
Fie 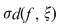 o asemenea sumă Riemann şi în care punctele intermediare o asemenea sumă Riemann şi în care punctele intermediare 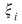 au fost alese iraţionale. Atunci au fost alese iraţionale. Atunci 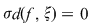 şi, prin urmare, şi, prin urmare, 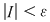 pentru orice pentru orice 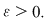
Va rezulta că 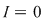 . Analog, pentru o sumă Riemann . Analog, pentru o sumă Riemann 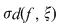 cu cu 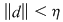 şi în care punctele intermediare au fost alese raţionale am avea şi în care punctele intermediare au fost alese raţionale am avea 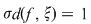 şi, prin urmare, şi, prin urmare, 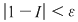 pentru orice pentru orice 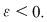
Ar rezulta că 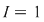 şi s-ar ajunge la o contradicţie. şi s-ar ajunge la o contradicţie.
Propoziţie : Orice funcţie integrabilă este mărginită.
Demonstraţie : Fie 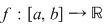 o funcţie integrabilă. Există atunci o funcţie integrabilă. Există atunci 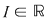 şi pentru orice şi pentru orice 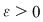 există există 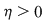 astfel încât pentru orice sumă Riemann astfel încât pentru orice sumă Riemann 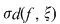 cu cu 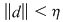 să avem să avem 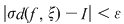 . Dacă fixăm o asemenea diviziune . Dacă fixăm o asemenea diviziune 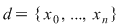 cu cu 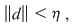 atunci pentru orice sistem de puncte intermediare atunci pentru orice sistem de puncte intermediare 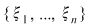 avem avem 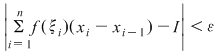 , de unde , de unde 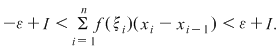
Materiale Didactice Asemanatoare
 Functii integrabile - Partea II Functii integrabile - Partea II
 Functii integrabile - Partea III Functii integrabile - Partea III
 Functii integrabile - Partea IV Functii integrabile - Partea IV
 Functii integrabile - Partea V Functii integrabile - Partea V
Bibliografie
| 1. Manual pentru clasa a XII-a - Nastasescu C., Nita C., Grigore Gh., Burlacu D. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a XII-a - Boboc N., Colojoara I. - Editura: Didactica si Pedagogica |
|