Monotonia functiei de gradul al II-lea - Varianta II
Autor: Dana Schiopu
Descriere: articol pentru Clasa a IX-a publicat in data de 26 Mar 2008, nivel de dificultate  . .
Intervalele de monotonie ale functiei de gradul doi cu discutie dupa semnul coeficientului termenului dominant, tabele de variatie, rata cresterii (descresterii) functiei, exemple.
Domenii: Functia de Gradul al II-lea
Demonstrăm 1 (pentru 2 se procedează analog).
Fie 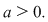 Dacă Dacă 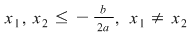 atunci atunci 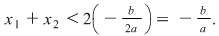
De aici 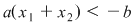 sau sau 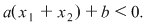
Aşadar 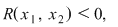 ceea ce arată că pe ceea ce arată că pe 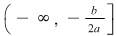 funcţia este strict descrescătoare. funcţia este strict descrescătoare.
Dacă 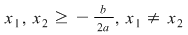 atunci atunci 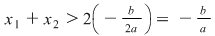 iar de aici iar de aici 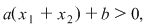 ceea ce arată că ceea ce arată că 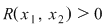
Deci 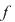 este strict crescătoare pe este strict crescătoare pe 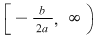 . Pentru a arăta că . Pentru a arăta că 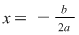 este punct de minim, iar este punct de minim, iar 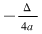 este valoarea minimă a funcţiei, utilizăm monotonia lui este valoarea minimă a funcţiei, utilizăm monotonia lui 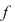 demonstrată mai sus. demonstrată mai sus.
Dacă 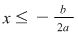 atunci ( atunci (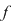 este descrescătoare) rezultă este descrescătoare) rezultă 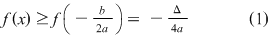
Dacă 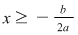 atunci ( atunci (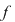 este crescătoare) rezultă este crescătoare) rezultă 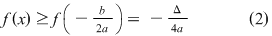
Din (1) şi (2) deducem că 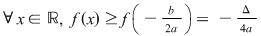
Notăm 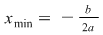 punctul de minim al funcţiei, iar punctul de minim al funcţiei, iar 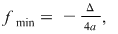
valoarea minimă a funcţiei 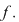
Dacă 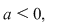 atunci atunci 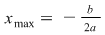 este punctul de maxim al funcţiei, este punctul de maxim al funcţiei,
iar 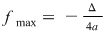 reprezintă valoarea maximă a funcţiei reprezintă valoarea maximă a funcţiei 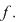

Materiale Didactice Asemanatoare
 Aplicatii ale monotoniei functiei de gradul al II-lea Aplicatii ale monotoniei functiei de gradul al II-lea
 Aplicatii pentru graficul functiei de gradul al II-lea Aplicatii pentru graficul functiei de gradul al II-lea
 Definitia functiei de gradul al II-lea. Grafic prin puncte Definitia functiei de gradul al II-lea. Grafic prin puncte
 Forma canonica a functiei de gradul al II-lea Forma canonica a functiei de gradul al II-lea
 Graficul functiei de gradul al II-lea Graficul functiei de gradul al II-lea
 Graficul functiei de gradul al II-lea - varianta II Graficul functiei de gradul al II-lea - varianta II
 Minimul si maximul functiei de gradul al II-lea Minimul si maximul functiei de gradul al II-lea
 Monotonia functiei de gradul al II-lea Monotonia functiei de gradul al II-lea
 Reprezentarea grafica a unei restrictii Reprezentarea grafica a unei restrictii
 Semnul functiei de gradul al II-lea Semnul functiei de gradul al II-lea
Bibliografie
| 1. Manual pentru clasa a IX-a - Ganga M. - Editura: Mathpress (anul 2003) |
|