Semnul functiei de gradul al II-lea - varianta II
Autor: Dana Schiopu
Descriere: articol pentru Clasa a IX-a publicat in data de 26 Mar 2008, nivel de dificultate  . .
Intervalele de monotonie ale functiei de gradul doi cu discutie dupa semnul coeficientului termenului dominant, tabele de variatie, interpretare geometrica: semnul functiei in regiunile din plan determinate de parabola, figuri , exemple.
Domenii: Functia de Gradul al II-lea
Demonstraţie:
Vom demonstra teorema pentru 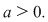
Cazul 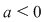 se tratează analog. se tratează analog.
1. Am văzut că dacă binomul de gradul al doilea 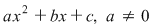 are rădăcinile diferite are rădăcinile diferite 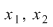 , atunci se poate scrie , atunci se poate scrie 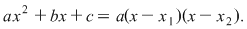
Din 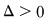 rezultă că ecuaţia ataşată are două rădăcini reale diferite rezultă că ecuaţia ataşată are două rădăcini reale diferite 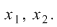
Deci funcţia 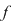 se poate scrie se poate scrie 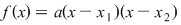
Presupunem 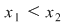
Dacă 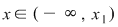 atunci atunci 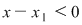 şi şi 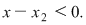
Ţinând seama de regula semnelor la înmulţire rezultă 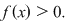
Dacă 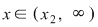 atunci atunci 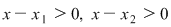 şi şi 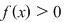 . .
Am arătat astfel că dacă 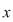 este în afara rădăcinilor, adică dacă este în afara rădăcinilor, adică dacă 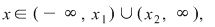 atunci atunci 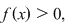 adică adică 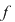 are acelaşi semn cu are acelaşi semn cu 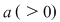
Dacă 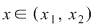 atunci atunci 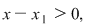 iar iar 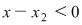
Prin urmare 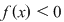 adică adică între zerourile adică adică între zerourile 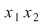 funcţia funcţia 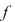 ia valori de semn contrar lui ia valori de semn contrar lui 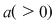
2. În acest caz, dacă 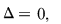 ecuaţia ataşată are rădăcină dublă ecuaţia ataşată are rădăcină dublă 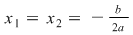 şi funcţia şi funcţia 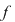 se exprimă sub forma se exprimă sub forma 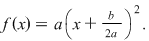
Dacă 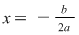 atunci atunci 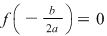
Dacă 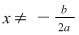 atunci atunci 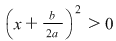 şi cum şi cum 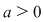 avem avem 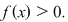
Prin urmare semnul lui 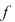 este acelaşi cu semnul lui este acelaşi cu semnul lui 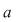 pe pe 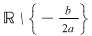 . .
3. Dacă 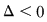 atunci scriem funcţia atunci scriem funcţia 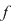 sub formă canonică şi avem: sub formă canonică şi avem:
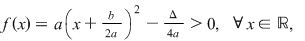 evident. evident.
Materiale Didactice Asemanatoare
 Aplicatii ale monotoniei functiei de gradul al II-lea Aplicatii ale monotoniei functiei de gradul al II-lea
 Aplicatii pentru graficul functiei de gradul al II-lea Aplicatii pentru graficul functiei de gradul al II-lea
 Definitia functiei de gradul al II-lea. Grafic prin puncte Definitia functiei de gradul al II-lea. Grafic prin puncte
 Forma canonica a functiei de gradul al II-lea Forma canonica a functiei de gradul al II-lea
 Graficul functiei de gradul al II-lea Graficul functiei de gradul al II-lea
 Graficul functiei de gradul al II-lea - varianta II Graficul functiei de gradul al II-lea - varianta II
 Minimul si maximul functiei de gradul al II-lea Minimul si maximul functiei de gradul al II-lea
 Monotonia functiei de gradul al II-lea Monotonia functiei de gradul al II-lea
 Monotonia functiei de gradul al II-lea - Varianta II Monotonia functiei de gradul al II-lea - Varianta II
 Semnul functiei de gradul al II-lea Semnul functiei de gradul al II-lea
Bibliografie
| 1. Manual pentru clasa a IX-a - Ganga M. - Editura: Mathpress (anul 2003) |
|