 Optiuni  Inapoi la biblioteca  Da un Test Nou |
Elemente de combinatorica si aplicatii
Autor: Dana Schiopu
Descriere: articol pentru Clasa a X-a publicat in data de 14 Apr 2008, nivel de dificultate  . .
Aplicatii ale calculului cu combinari: identitati; mica teorema a lui Fermat cu aplicatii, principiul excluderii si includerii cu aplicatii; sumele puterilor asemenea a primelor numere naturale cu demonstratii.
Domenii: Elemente de combinatorica
Observaţie:
Dacă 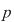 este un număr natural prim, iar este un număr natural prim, iar 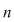 un număr natural care nu este multiplu de un număr natural care nu este multiplu de 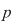 , atunci , atunci 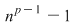 se divide cu se divide cu 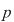 . .
Exemple:
1) Deoarece 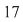 este număr prim, atunci este număr prim, atunci 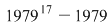 se divide cu se divide cu 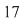 . .
2) Deoarece 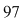 este număr prim, iar este număr prim, iar 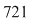 nu este multiplu de nu este multiplu de 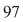 , atunci , atunci 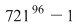 se divide cu se divide cu 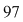 . .
(2). Principiul includerii şi excluderii.
Considerăm mulţimile finite.
Dacă 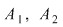 sunt două mulţimi nevide, atunci egalitatea sunt două mulţimi nevide, atunci egalitatea
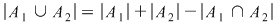 se numeşte formula includerii şi excluderii, numită aşa deoarece unele elemente se includ şi într-o mulţime şi în alta, iar altele se elimină. se numeşte formula includerii şi excluderii, numită aşa deoarece unele elemente se includ şi într-o mulţime şi în alta, iar altele se elimină.
Această formulă este adevărată, deoarece în 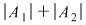 intră de două ori elementele comune ale lui intră de două ori elementele comune ale lui 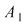 şi şi  , iar în , iar în 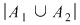 o singură dată. De aceea, în membrul drept se scade numărul acestor elemente comune. o singură dată. De aceea, în membrul drept se scade numărul acestor elemente comune.
Formula rămâne adevărată şi dacă se înlocuieşte 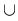 cu cu  şi şi  cu cu 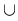 , când avem, de asemenea, formula includerii şi excluderii: , când avem, de asemenea, formula includerii şi excluderii:
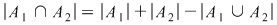 , ceea ce se vede uşor şi se obţine din formula precedentă. Pentru cazul a trei mulţimi formula includerii şi excluderii are forma: , ceea ce se vede uşor şi se obţine din formula precedentă. Pentru cazul a trei mulţimi formula includerii şi excluderii are forma:

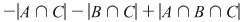
Formula corespunzătoare se obţine uşor de aici prin dualitate.
Materiale Didactice Asemanatoare
 Aranjamente Aranjamente
 Binomul lui Newton Binomul lui Newton
 Combinari Combinari
 Elemente de combinatorica Elemente de combinatorica
 Identitati in calculul cu combinari Identitati in calculul cu combinari
 Multimea functiilor f definite pe A cu valori in B, unde A si B sunt multimi finite Multimea functiilor f definite pe A cu valori in B, unde A si B sunt multimi finite
 Multimea functiilor injective si bijective Multimea functiilor injective si bijective
 Permutari. Multimi ordonate cu n elemente Permutari. Multimi ordonate cu n elemente
Bibliografie
| 1. Manual pentru clasa a X-a - Nastasescu C., Nita C., Popa S. - Editura: Didactica si Pedagogica | | 2. Manual pentru clasa a X-a - Chiles C, Constantinescu G., Ilie R., Marinescu I - Editura: Sigma | | 3. Manual pentru clasa a X-a - Algebra - Ganga M. - Editura: MathPress | | 4. Probleme de algebra - Schneider Gh., Schneider V. - Editura: Apolo - Oltenia |
|